 STACK
STACK
STACK is an assessment system for mathematics, science and related disciplines, designed to enable students to answer questions with a mathematical expression, such as Arithmetic expressions, Fractional expressions, Algebraic expression and much more.
- Students type in mathematical expressions, and are not restricted to multiple choice.
- Separate validation and assessment with an emphasis on formative assessment.
- Random generation of questions.
- A wide variety of input types, including line by line working.
- Support for multipart questions.
- Support for scientific units and significant figures
Main features
Equivalent answers of the right form
STACK can accept equivalent expressions, for example (x+1)2=x2+2x+1. STACK can also establish the form of an answer, for example if it is factorised. STACK is designed to let teachers specify independent properties required in an answer.
Ask for examples
The system can mark questions that ask the student to provide an example.
Give an example of a function f(x) with a minimum at x=0 and a maximum at x=2. Rather than comparing the student's answer to the teacher's answer, STACK checks that the answer has the required properties. Giving examples is a higher-order skill that is impossible to assess with conventional Computer Aided Assessment (CAA) systems.
Intelligent randomisation
Randomising questions is invaluable in ensuring students can practice and reducing sharing of answers. The trick is to reverse-engineer the randomised question from a randomised answer. Computer algebra is invaluable to support this process.
Give feedback and partial credit
Consider a question like: Give an example of a cubic polynomial with the following properties:
- p(0)=1,
- p(x)=0 at x=2 and at x=3.
Here, STACK can check each condition separately on the student's answer and assign partial credit accordingly. If the student gave the answer p(x)=x2−5x+6 for example, then STACK could reply: Your answer does have zeros at the required points but its value at zero is not equal to 1. You received 2 out of 3 points. Please try again. There are a variety of ways in which feedback can be given, including plotting the students' answer against the teacher's answer.
Multipart questions
STACK supports multipart questions, like the following:
(a) differentiate x2+5x with respect to x.
(b) substitute x=5 into your answer.
You can have follow-through marking for situations where, for example, the student enters a wrong expression to part (a), but correctly substitutes in values into their expression in part (b). Here, STACK can recognise the work the student put into part (b), even though their answer is different from the "correct" answer.
Adding questions
STACK quiz questions are available to add to your quiz activities within UR Courses.
-
Create a new quiz activity. If you aren't sure how to create a quiz activity please refer to adding a quiz to your course.
-
Once the quiz has been created,
- click the Edit quiz button,
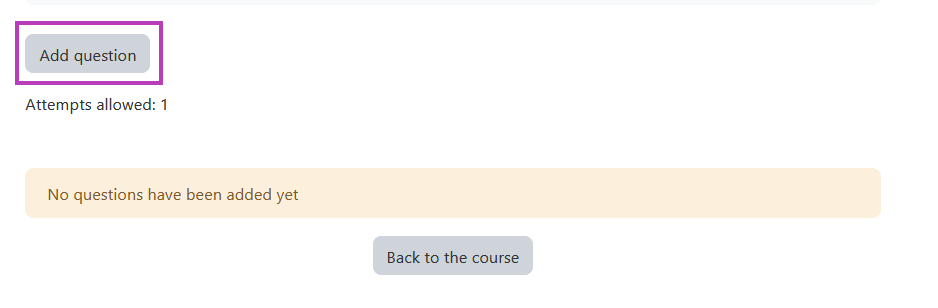
- or click the action menu button, in the top right corner of the quiz, and click edit quiz button as highlighted on the image below.
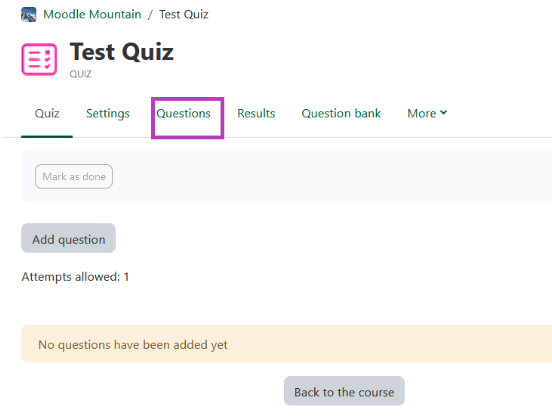
- To add a question, click the add link button and then click Add new question.
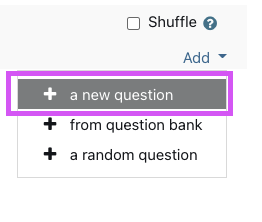
- Choose question type popup window will open, scroll down to the bottom of the popup window and the stack question type should be presented as highlighted on the image below.
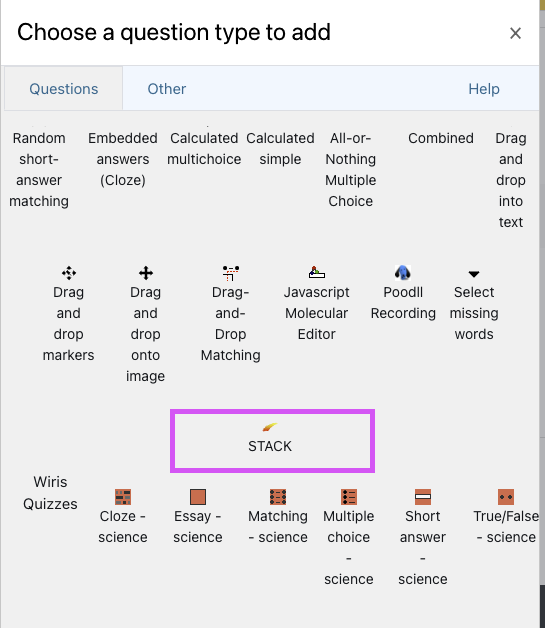
- click the Edit quiz button,
- Please visit STACK Docs? A detailed documentation of STACK and resource.
Question tips and reference
There are many ways to organize and setup STACK questions within your course. The following are some helpful video references created by the STACK project.
- Please visit Writing quality STACK questions? A detailed stack video reference and resource provided by STACK.
- Please visit Make STACK questions look nice? A detailed stack video reference and resource provided by STACK.
Project demo
The STACK project has a public demo which provides some example and sample STACK questions that can help get you started using STACK.
The rest of this course contains sample collections of quizzes on common topics, such as Calculus and Algebraic manipulation.
This course also contains a large number of additional questions which are not collected into quizzes.
Tip: We recommend to start from the beginning of the demo then work your way trough. Because there will be enrolment key's at the last topics that you can used to unlock other resources of the STACK Demo.
Example content of STACK Demo
- Learning to use STACK for students The following questions are designed to help students understand the STACK layout and syntax.
- Demonstration quiz
- Authoring features These quizzes demonstrate various authoring features in STACK.
- Sample collections
- Diagnostic tests In April 2010 the National HE STEM Programme funded a mini-project to take existing diagnostic tests in core mathematics and develop similar automatic tests for the STACK computer aided assessment system.
Useful URL
STACK demonstration site URL
STACK demo Login URL
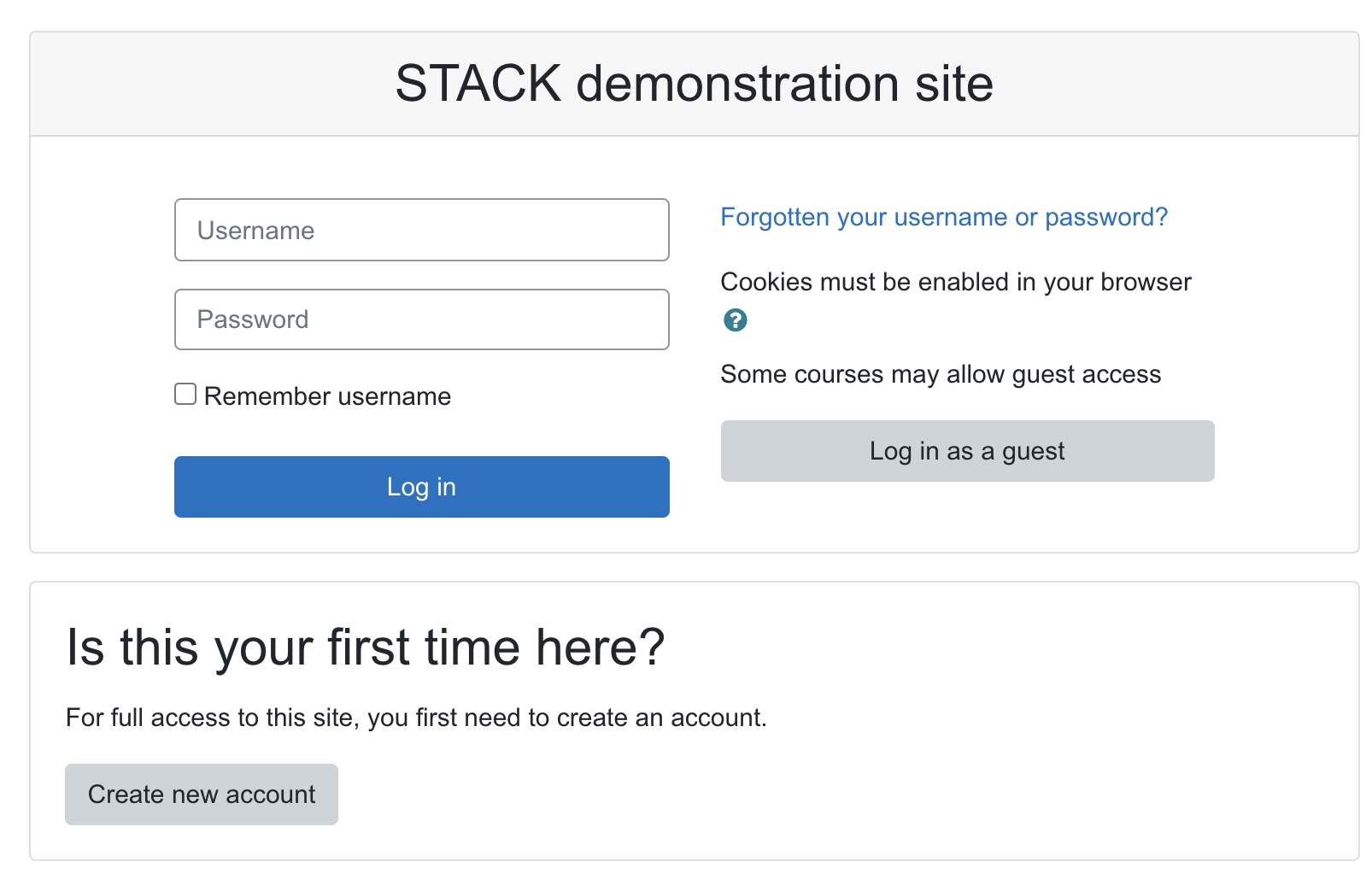
To be able to access the content of this demo course page. You need to create an account signup here.
Quiz samples
Feel free to try out quiz samples that is available in UR Courses and you can copy this as well in github and import it via xml.
STACK-4.3.9-demo is available in UR Courses
Note: Full access to the course page will need additional user privileges. Please notify IT-Support to get access to the Stack demo course page.
Quiz Examples availble in Testing Course page.
- JSXGraph-block-tech-samples
- Equivalence_reasoning_example
- input-sample-questions
- Reveal_block_example
- Sample_questions
- V4-syntax-samples
Tip: All the quiz questions and answers has been commented out to give more information and ideas on how the question is being used in STACK.
Additional documentation
Visit the full documentation provided by STACK project
Stack documentation
Getting started with STACK
Student errors
Common student errors: theory and discussion -- Ian Jones
Addressing common student errors
Addressing common student errors in STACK --Chris Sangwin
What is Maxima
Maxima is a system for working with expressions, such as x+y, sin(a+bπ), and u · v − v · u.
Maxima is not much worried about the meaning of an expression. Whether an expression is meaningful is for the user to decide.
Sometimes you want to assign values to the unknowns and evaluate the expression. Maxima is happy to do that. But Maxima is also happy to postpone assignment of specific values; you might carry out several manipulations of an expression, and only later (or never) assign values to unknowns.

Introduction to Maxima with STACK - Chris Sangwin
Tip: Familiarization on how to use MAXIMA will help you understand a bit more on how to write mathematical notation in UR Courses using STACK.